Формулы нормальных и касательных напряжений на наклонных площадках, проходящих через рассматриваемую точку
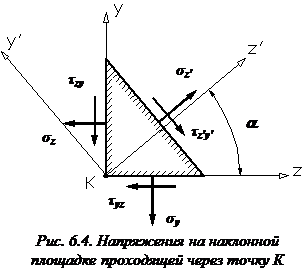При изучении плоского напряженного состояния будем рассматривать только наклонные площадки, которые перпендикулярны граням параллелепипеда, на которых отсутствуют нормальные и касательные напряжения (рис. 6.4).
Положение наклонной площадки определяется углом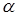 
, образующим внешнюю нормаль 
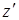к этой площадке с осью z. Угол 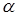положителен, если отсчитывается против хода часовой стрелки.
Нормальные и касательные напряжения на наклонной площадке, проходящей через точку К, определяются по формулам:
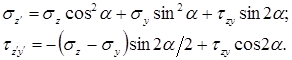
Из формул нормальных и касательных напряжений на наклонных площадках, проходящих через рассматриваемую точку, видно: напряжения в наклонных площадках являются непрерывными функциями угла 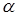и могут иметь экстремальные значения: максимумы и минимумы.
Найдем угол наклона площадки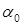 
, при котором нормальное напряжение 
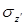принимает экстремальное значение.
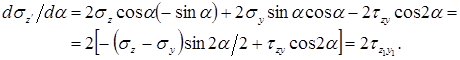
Приравняем формулу к нулю. Получим формулу экстремального значения угла наклона площадки:
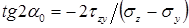
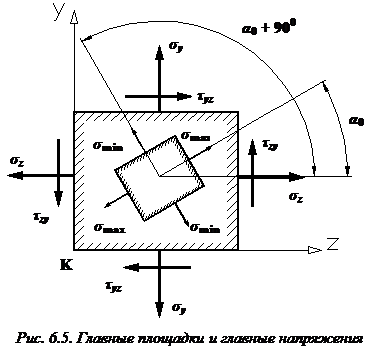Найдем углы 
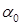и 
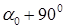, определяющие положение двух взаимно перпендикулярных площадок, на которых возникают экстремальные нормальные напряжения 
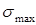и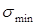 
в рассматриваемой точке К (рис. 6.5).
 |
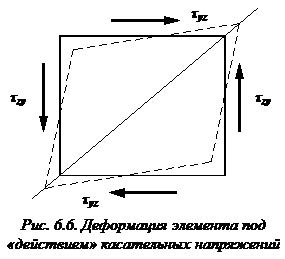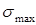всегда направлено в сторону, где сходятся касательные напряжения 
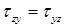. (см. рис. 6.6.) Касательные напряжения «создают» дополнительное удлинение одной из диагоналей.