Решение типовых задач по сопромату.
Напряженное состояние в точке тела - пример решения задачи
Пример решения задачи напряженное состояние в точке тела – условие задачи
Дано 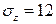 кН/см2,
кН/см2, 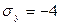 кН/см2,
кН/см2, 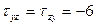 кН/см2 (рис. 3.6, а). Найти главные напряжения
кН/см2 (рис. 3.6, а). Найти главные напряжения 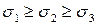 , направления главных площадок и максимальное касательное напряжение
, направления главных площадок и максимальное касательное напряжение 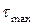 .
.
Пример решения задачи напряженное состояние в точке тела – расчетная схема
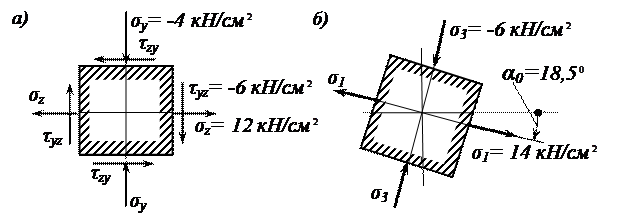 Рис. 3.6
Рис. 3.6
Решение примера задачи на напряженное состояние в точке тела
Напомним правила знаков для нормальных и касательных напряжений.Нормальное напряжение, соответствующее растяжению, считается положительным, а сжатию – отрицательным.
Касательное напряжение считается положительным, если одновременно выполняются (или одновременно не выполняются) следующие два условия:
направление напряжения совпадает с положительным направлением соответствующей координатной оси;
внешняя нормаль к площадке, на которой оно возникает, направлена в ту же сторону, что и другая, соответствующая, координатная ось.
Определяем главные напряжения, возникающие на трех главных площадках, проходящих через рассматриваемую точку твердого тела
Для плоского напряженного состояния одно из главных напряжений, возникающее на площадке с нормалью x, равно нулю.
Вычисляем значения двух других главных напряжений:
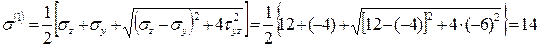 кН/см2;
кН/см2;
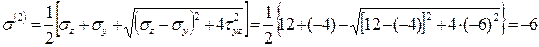 кН/см2.
кН/см2.
Учитывая, что 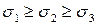 , окончательно имеем:
, окончательно имеем:
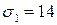 кН/см2,
кН/см2, 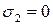 ,
, 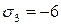 кН/см2.
кН/см2.
Делаем проверку (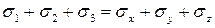 ):
):
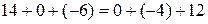 или
или 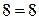 ,
,
то есть верно.
Находим положение главных площадок
Углы 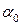 и
и 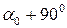 , определяющие положение двух взаимно перпендикулярных площадок, на которых возникают главные напряжения
, определяющие положение двух взаимно перпендикулярных площадок, на которых возникают главные напряжения 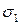 и
и 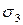 , определяются из формулы
, определяются из формулы
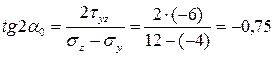 .
.
Отсюда: 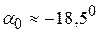 и
и 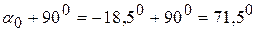 .
.
Напомним, что угол считается положительным, если он отсчитывается от оси z против хода часовой стрелки.
Найденные углы (см. рис. 3.6, б) определяют и направления «действия» главных напряжений 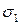 и
и 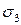 .
.
Определяем наибольшее касательное напряжение, возникающее в рассматриваемой точке тела
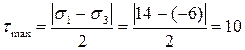 кН/см2.
кН/см2.
Оно «действует» на площадке, которая наклонена под углом 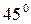 к первой и третьей главным площадкам.
к первой и третьей главным площадкам.
Пример задачи для самостоятельного решения – напряженное состояние в точке тела

Условие задачи "напряженное состояние в точке тела"
Из нагруженного твердого тела, находящегося в равновесии, около некоторой точки выделен элементарный параллелепипед со сторонами 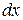 ,
, 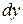 и
и 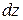 . Считается, что на двух его параллельных гранях с нормалью x нормальные
. Считается, что на двух его параллельных гранях с нормалью x нормальные 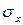 и касательные напряжения
и касательные напряжения 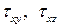 отсутствуют, то есть напряженное состояние является плоским. Вместо объемного параллелепипеда, с целью упрощения, на рис. 3.5 показан плоский элемент: его проекция на плоскость
отсутствуют, то есть напряженное состояние является плоским. Вместо объемного параллелепипеда, с целью упрощения, на рис. 3.5 показан плоский элемент: его проекция на плоскость 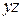 . Штриховкой указана внутренняя область элемента. Требуется найти главные напряжения
. Штриховкой указана внутренняя область элемента. Требуется найти главные напряжения 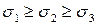 , направления главных площадок и максимальное касательное напряжение
, направления главных площадок и максимальное касательное напряжение 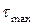 .
.
Исходные данные к задаче напряженное состояние в точке тела
| вариант |
|
|
|
| 1 | 10 | 6 | –3 |
| 2 | 2 | –7 | 7 |
| 3 | 3 | 6 | –6 |
| 4 | 4 | –5 | 5 |
| 5 | 5 | 4 | –4 |
| 6 | 6 | 3 | 3 |
| 7 | 7 | 2 | –2 |
| 8 | –7 | –1 | 1 |
| 9 | –6 | –2 | –7 |
| 10 | –5 | 3 | 6 |
| 11 | –4 | 4 | –5 |
| 12 | –3 | 5 | 4 |
| 13 | –2 | 6 | –3 |
| 14 | –10 | 7 | 2 |
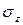 , кН/см2
, кН/см2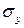 , кН/см2
, кН/см2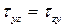 , кН/см2
, кН/см2