Перемещения при изгибе

Чтобы судить о работе балок, недостаточно знать только напряжения, которые возникают в ней при деформировании.

Прочные балки могут оказаться непригодными к эксплуатации из-за недостаточной жесткости. Если балка сильно прогибается под нагрузкой, то в ней могут возникнуть колебания с большими амплитудами, приводящие к дополнительным напряжениям.

Для проверки жесткости балки необходимо уметь определять перемещения при изгибе отдельных точек ее оси.

В результате изгиба ось балки становится криволинейной. Кривизна оси балки:

.

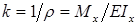Произвольная точка, лежащая на оси балки переместится в направлении вертикальной оси y и продольной оси z. Вертикальное перемещение при изгибе будем обозначать буквой v и называть прогибом балки. Продольное перемещение при изгибе точки будем обозначать буквой u.

Касательная, проведенная к точке, расположенной на изогнутой оси балки, будет повернута по отношению к прямолинейной оси на некоторый угол 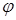. Этот угол, очевидно, равен углу поворота поперечного сечения балки 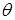, проходящего через рассматриваемую точку. Величины u, v и 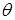являются компонентами перемещения произвольного поперечного сечения.

Проверка жесткости балки при изгибе сводится к требованию, согласно которому наибольший ее прогиб (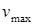) не должен превышать определенной доли от пролета балки (l): .

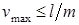Здесь число m устанавливается нормами проектирования и колеблется обычно в пределах от 300 до 1000. Для ответственных сооружений, например, для мостов, 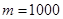. Прогибы балки при изгибе малы по сравнению с ее пролетом. Это позволяет ввести некоторые упрощения:

во-первых, при малых вертикальных перемещениях (прогибах v) угол наклона касательной к изогнутой оси балки и угол поворота поперечного сечения балки: 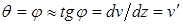. Угол поворота поперечного сечения равен первой производной от прогиба балки;

во-вторых, горизонтальным перемещением (u) можно пренебречь, так как оно по сравнению с прогибом (v) и углом поворота поперечного сечения (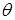), является величиной более высокого порядка малости (можно считать, что каждая точка оси балки перемещается только по вертикали).

Таким образом, для определения полной картины деформации при изгибе необходимо получить уравнение оси изогнутой балки: .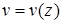

Если уравнение оси изогнутой балки известно, можно построить кривую прогибов и найти наибольший прогиб, который позволит нам судить о жесткости балки.

В ряде задач возникает необходимость и в определении угла поворота поперечного сечения.