Теорема Кастильяно

Формулировка теоремы Кастильяно: Перемещение точки приложения обобщенной силы по направлению ее действия равно частной производной от потенциальной энергии деформации по этой силе .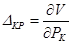

Для определения перемещения (линейного или углового) в точке, где по условию задачи внешнее усилие (сила или момент) отсутствует, необходимо приложить в этом месте фиктивную обобщенную силу. Далее следует написать выражение для потенциальной энергии деформации от всех сил, включая и фиктивную, и взять от этого выражения производную по фиктивной силе. В полученном выражении для обобщенного перемещения фиктивную нагрузку необходимо принять равной нулю.

применение теоремы Кастильяно на примере

Теорема Кастильяно – определение перемещений

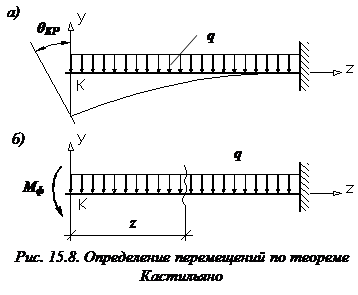
Определим, используя теорему Кастильяно, угол поворота поперечного сечения в точке K жестко защемленной балки, нагруженной распределенной нагрузкой q (рис. 15.8, а).

Приложим к заданной балке на ее свободном конце в точке K фиктивный момент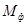(рис. 15.8, б).

Изгибающий момент в произвольном сечении такой балки равен: .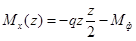

Потенциальная энергия деформации при изгибе балки (при пренебрежении влиянием перерезывающей силы) вычисляется по формуле:

.

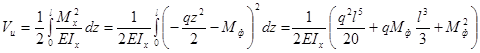Угол поворота равен:

.

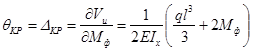Принимая в полученном выражении 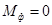, окончательно найдем:

.

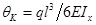Теорема Кастильяно - раскрытие статической неопределимости

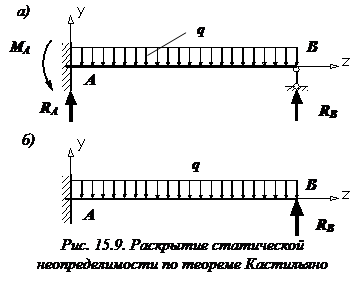
Теорему Кастильяно можно использовать и для раскрытия статической неопределимости. Рассмотрим, например, один раз статически неопределимую балку (рис. 15.9, а).

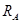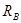Для определения опорных реакций (и ), а также момента в жесткой заделке (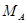) мы имеем только два уравнения статик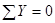и:

и .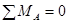

Мысленно удалим лишнюю связь – правую опору и вместо нее введем в рассмотрение неизвестную опорную реакцию 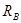, которую мы будем рассматривать, как активную силу (рис. 15.9, б). Однако перемещение полученной таким образом статически определимой балки в точке приложения силы 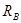должно быть равно нулю, то есть

.

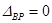Составим выражение для изгибающего момента в произвольном сечении статически определимой балки:

.

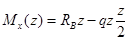Потенциальная энергия деформации балки будет равна:

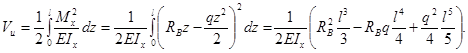
Так как перемещение в месте приложения неизвестной силы 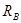равно нулю, то

,

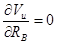тогда

.

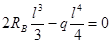Решая полученное уравнение, находим реакцию правой опоры:

.

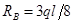Теперь, составляя уравнения статики, легко определяем остальные две опорные реакции:

;

.
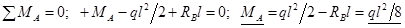
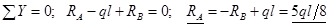