Удар

Удар - это происходящее в результате соприкосновения взаимодействие движущихся тел.

Удар – что характерно для него?

Удар характеризуется резким изменением скоростей частиц взаимодействующих тел за малый промежуток времени, при этом сила удара достигает очень большого значения. В качестве примера можно привести действие кузнечного молота на кусок металла, удар падающего груза при забивке свай, воздействие колеса вагона на рельс при перекатывании через стык.

Удар – допущения при расчете

За время совершения удара очень трудно произвести измерения, связанные с определением силы удара. Поэтому обычно производится условный расчет на удар, по которому определяются внутренние силы и перемещения, возникающие в стержне. Сначала определяется наибольшее динамическое перемещение точки стержня, по которой наносится удар, а затем определяется напряженное состояние стержня.

Существуют следующие допущения при расчете стержня на удар:

Допущение 1: деформация стержня, вызванная ударной нагрузкой, описывается законом Гука, а сам стержень является линейно деформируемой системой. При этом модуль Юнга имеет такое же значение, как и при статическом нагружении стержня;

Допущение 2: работа, совершаемая падающим грузом, полностью переходит в потенциальную энергию деформации стержня;

Допущение 3: масса стержня, воспринимающего удар, пренебрежимо мала по сравнению с массой падающего груза;

Допущение 4: удар считается неупругим.

Динамический прогиб при ударе

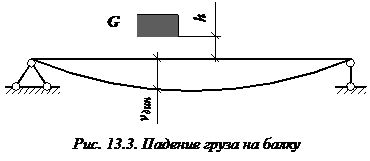
Рассмотрим удар груза весом G, падающего с высоты h на балку (рис. 13.3).

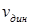Обозначим – динамический прогиб балки в месте падения груза.

Работа, совершаемая падающим грузом, равна: 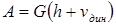. Согласно допущению 2, работа полностью переходит в потенциальную энергию деформации балки (V). По теореме Клапейрона потенциальная энергия деформации равна половине произведения некоторой динамической силы (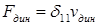) на соответствующее ей динамическое перемещение (): .

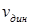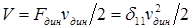Учитывая, что статический прогиб балки в месте падения груза G, вызванный его статическим приложением, равен 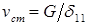, получим уравнение динамического прогиба балки: 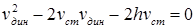. Отсюда .

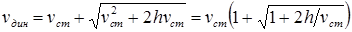Динамический прогиб балки в месте падения груза: 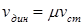, где 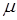– коэффициент динамичности. .

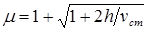Допущение 1 позволяется сделать вывод, что динамические напряжения от действия ударной нагрузки во столько же раз больше напряжений при статической нагрузке, во сколько раз динамический прогиб больше статического: .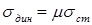

Когда высота падения 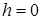(внезапное приложение нагрузки), .

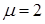Для уменьшения коэффициента динамичности необходимо увеличить 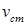, поэтому для смягчения удара применяют пружинные и резиновые прокладки, допускающие большие деформации.