Расчет стержня на устойчивость. Коэффициент продольного изгиба

При назначении размеров длинного сжатого стержня, в первую очередь, приходится заботиться о том, чтобы он в процессе эксплуатации не потерял устойчивость прямолинейной формы равновесия. Напряжения в сжатом стержне не должны превышать критических напряжений: .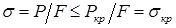

Исследования показали: незначительные местные ослабления стержня (например, заклепочными отверстиями) не оказывают существенного влияния на значение критической нагрузки, поэтому в формуле 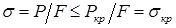берется вся площадь поперечного сечения.

Условие прочности при сжатии:

.

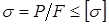Расчет сжатого стержня на устойчивость можно привести по форме к расчету на простое сжатие. Необходимо учесть, что длинный стержень (большой гибкости) потеряет устойчивость при меньшем напряжении, чем допускаемое напряжение 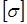. Условие устойчивости сжатого стержня: 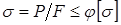, где 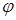- коэффициент продольного изгиба. Коэффициент продольного изгиба зависит от материала стержня и его гибкости 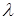, и изменяется в пределах от 0 (при 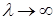) до 1 (при ).

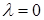Этот метод расчета не связан с пределами применимости формулы Эйлера и может быть использован практически при всех значениях гибкости.

Проектировочный расчет по условию устойчивости сжатого стержня 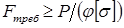, связанный с подбором размеров поперечного сечения стержня, приходится осуществлять методом последовательных приближений. Это обусловлено тем, что площадь поперечного сечения стержня в неявном виде входит и в правую часть выражения требуемой нагрузки 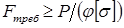, поскольку коэффициент продольного изгиба (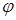) зависит от гибкости стержня (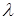), а она - от радиуса инерции: .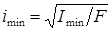