Статически неопределимые системы

Статически неопределимые системы – это системы, для которых из уравнений статики не удается определить все опорные реакции.

Пример статически неопределимой системы

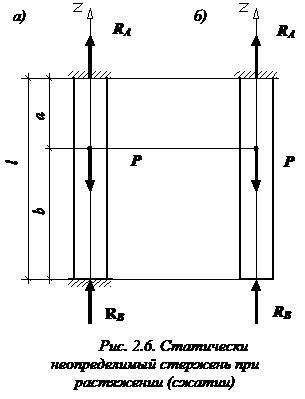
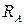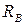Рассмотрим стержень (рис. 2.6, а) и назовем заданной системой. Нагруженный стержень заделан обоими концами. В заделках возникают две реакции, направленные вдоль оси стержня: и . Для их определения мы имеем только одно уравнение статики: 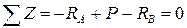, в которое входят две неизвестные реакции.

Для раскрытия статической неопределимости заданной системы необходимо записать дополнительное уравнение – уравнение перемещений.

Отбросим нижнюю заделку и заменим ее действие на стержень некоторой силой 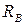, которую мы в дальнейшем будем рассматривать как активную силу (рис. 2.6, б). Полученный стержень назовем основной системой для дальнейшего расчета. Полученный таким образом стержень является уже статически определимым. Он заделан одним концом и нагружен двумя активными силами P и .

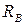Удлинение заданной системы равно нулю (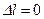), поэтому неизвестную силу 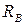найдем из условия, что и удлинение основной системы тоже равно нулю:

.

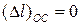Это и есть уравнение перемещений (свидетельствует об одинаковости деформаций заданной и основной систем).

Используя принцип суперпозиции, запишем удлинение основной системы в виде:

.

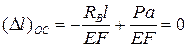Отсюда:

.

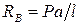Статическая неопределимость раскрыта, теперь вернемся к заданной системе.

Из уравнения статики находим вторую реакцию:

.

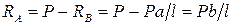Переходим к построению эпюры продольных сил, определению напряжений и деформаций в стержне, оценке его прочности и жесткости.