Эпюра продольных сил

Если продольные силы, возникающие в различных поперечных сечениях стержня, неодинаковы, закон их изменения по длине стержня представляется в виде графика N(z), называемого эпюрой продольных сил. Эпюра продольных сил необходима для оценки прочности стержня и строится для того, чтобы найти опасное сечение (поперечное сечение, в котором продольная сила принимает наибольшее значение ).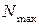

Как строить эпюру продольных сил?

Для построении эпюры N используется метод сечений. Продемонстрируем его применение на примере (рис. 2.1).

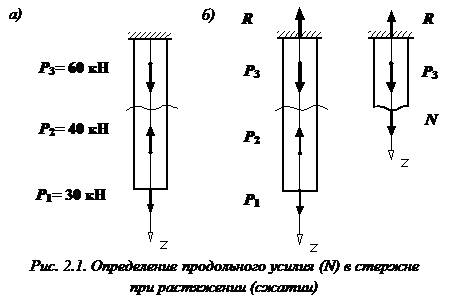Определим продольную силу N, возникающую в намеченном нами поперечном сечении стержня.

Разрежем стержень в этом месте и мысленно отбросим нижнюю его часть (рис. 2.1, а). Далее мы должны заменить действие отброшенной части на верхнюю часть стержня внутренней продольной силой N.

Для удобства вычисления ее значения закроем рассматриваемую нами верхнюю часть стержня листком бумаги. Напомним, что продольное усилие N, возникающее в поперечном сечении, можно определить как алгебраическую сумму всех продольных сил, действующих на отброшенную часть стержня, то есть на ту часть стержня, которую мы видим.

При этом применяем следующее правило знаков: силы, вызывающие растяжение оставленной части стержня (закрытой нами листком бумаги) входят в упомянутую алгебраическую сумму со знаком «плюс», а силы, вызывающие сжатие – со знаком «минус».

Итак, для определения продольной силы N в намеченном нами поперечном сечении необходимо просто сложить все внешние силы, которые мы видим. Так как сила 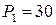кН растягивает верхнюю часть, а сила 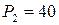кН ее сжимает, то 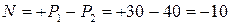кН.

Знак «минус» означает, что в этом сечении стержень испытывает сжатие.

Можно найти опорную реакцию R (рис. 2.1, б) и составить уравнение равновесия для всего стержня, чтобы проверить результат:

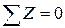
или

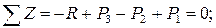
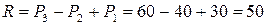кН.

Теперь заменим действие отброшенной нижней части неизвестным внутренним усилием N, направив его, например, от сечения, что соответствует растяжению.

Уравновешиваем оставленную нами верхнюю часть стержня:

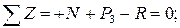
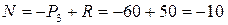кН.

Знак «минус» сигнализирует, что мы не угадали направление продольного усилия N. Оно будет не растягивающим, как мы предполагали, а сжимающим.

Таким образом, мы получили тот же самый результат.