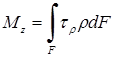Формула крутящего момента через касательные напряжения в поперечном сечении
В сопромате при повороте поперечного сечения каждая его точка (кроме, разумеется, точки, лежащей на оси вала) перемещается по некоторой дуге окружности радиуса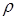 
. Поэтому направление касательного напряжения, возникающего в этой точке, должно быть перпендикулярно к радиусу 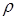, проведенному в эту точку.
Элементарная внутренняя касательная сила, возникающая на площадке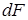 
(см. рис. 5.2), равна 
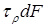, а момент внутренней касательной силы относительно оси 
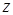(центра тяжести вала) характеризуется формулой:
.
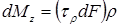Суммируя элементарные моменты касательной силы по всей площади, получим формулу крутящего момента через касательные напряжения, возникающего в поперечном сечении вала:
