Собственные моменты инерции при повороте осей координат
Пусть нам известны собственные моменты инерции 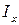 ,
, 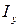 и
и 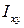 относительно двух взаимно перпендикулярных осей x и y, проходящих через центр тяжести C поперечного сечения стержня. Проведем через точку C другие оси
относительно двух взаимно перпендикулярных осей x и y, проходящих через центр тяжести C поперечного сечения стержня. Проведем через точку C другие оси 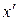 и
и 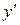 , повернутые относительно осей x и y на угол
, повернутые относительно осей x и y на угол 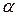 (рис. 4.3, б). Будем считать этот угол положительным при повороте осей координат против хода часовой стрелки.
(рис. 4.3, б). Будем считать этот угол положительным при повороте осей координат против хода часовой стрелки.
Моменты инерции поперечного сечения при повороте осей координат определяются по формулам:
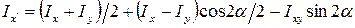 ;
;
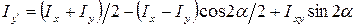
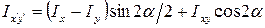 .
.
Из формул моментов инерции при повороте осей координат видно, что сумма собственных осевых моментов инерции не изменяется при повороте координатных осей: 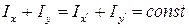
Две взаимно перпендикулярные оси, проходящие через центр тяжести фигуры, относительно которых центробежный момент инерции равен нулю, называются главными центральными осями инерции. Тогда из третьей формулы моментов инерции при повороте осей координат легко можно определить направление этих осей:
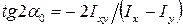
Из полученного выражения найдем два значения угла 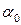 , которые отличаются друг от друга на угол
, которые отличаются друг от друга на угол 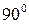 , которые определяют положение двух главных центральных осей.
, которые определяют положение двух главных центральных осей.