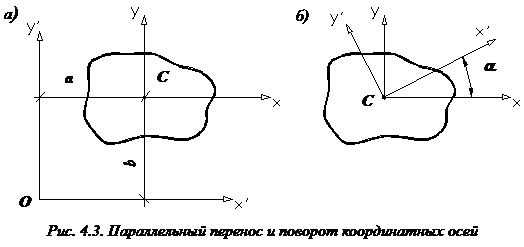
Момент инерции фигуры относительно параллельной оси. Переносные моменты инерции
Пусть две взаимно перпендикулярные оси x и y проходят через центр тяжести C поперечного сечения стержня. Проведем другие оси координат 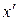 и
и 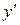 , параллельные осям x и y. Обозначим a и b координаты центра тяжести С в новых осях
, параллельные осям x и y. Обозначим a и b координаты центра тяжести С в новых осях 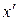 и
и 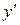 (рис. 4.3, а).
(рис. 4.3, а).
Тогда формулы осевых и центробежных моментов инерции фигуры относительно параллельных осей 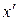 и
и 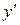 :
:
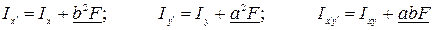
Первые слагаемые в формулах осевых и центробежных моментов инерции фигуры относительно параллельных осей названы собственными моментами инерции. Вторые (подчеркнутые) слагаемые называются переносными моментами инерции.
Отметим, что координаты a и b необходимо подставлять в формулы моментов инерции фигуры относительно параллельных осей с учетом их знаков, что является крайне важным для третьей из приведенных формул.
|
|