Внутренние силы при внецентренном сжатии
Рассмотрим, какие внутренние силы при внецентренном сжатии действуют на стержень в поперечном сечении. Пусть сжимающая сила (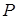 ) приложена в некоторой точке A с координатами
) приложена в некоторой точке A с координатами 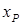 и
и 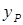 в главных центральных осях инерции x и y (см. рис. 10.1, а).
в главных центральных осях инерции x и y (см. рис. 10.1, а).
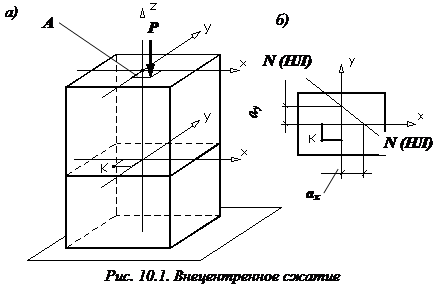 С учетом допущения, что стержень обладает большой жесткостью на изгиб:
С учетом допущения, что стержень обладает большой жесткостью на изгиб: 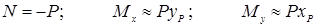 .
.
Формула изгибающих моментов при внецентренном сжатии с учетом прогибов:  , где
, где 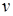 и
и 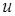 прогибы рассматриваемого поперечного сечения стержня в направлении осей
прогибы рассматриваемого поперечного сечения стержня в направлении осей 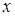 и
и 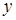 , соответственно. Наше допущение о большой жесткости стержня на изгиб заключается в предположении:
, соответственно. Наше допущение о большой жесткости стержня на изгиб заключается в предположении: 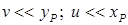 .
.
Нормальные напряжения в произвольной точке 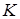 (см. рис. 10.1) с координатами
(см. рис. 10.1) с координатами 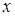 и
и 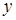 будут равны:
будут равны: 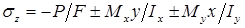 , где, согласно принципу независимости действия сил, первое слагаемое - напряжение от сжатия, а второе и третье – от изгиба.
, где, согласно принципу независимости действия сил, первое слагаемое - напряжение от сжатия, а второе и третье – от изгиба.
Значения изгибающих моментов и координат исследуемой точки 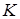 подставляются в формулу
подставляются в формулу  по абсолютному значению, а знак второго и третьего слагаемых определяется по физическому смыслу.
по абсолютному значению, а знак второго и третьего слагаемых определяется по физическому смыслу.