Наибольшие нормальные напряжения при косом изгибе

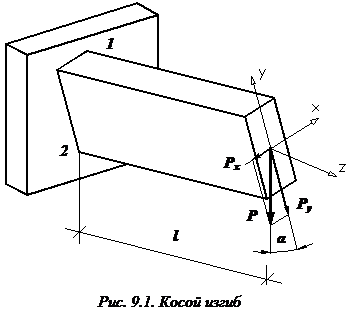
Рассмотрим консольную балку прямоугольного сечения длиной l, нагруженную вертикальной силой P (рис. 9.1). Главная центральная ось балки (ось симметрии) y составляет некоторый малый угол 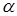с направлением действия нагрузки (наличие технологического брака).

Разложим силу P на составляющие: .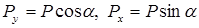

Воспользуемся принципом независимости действия сил и рассмотрим отдельно действие каждой составляющей.

Нагрузк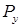и и 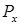вызывают в поперечном сечении, расположенном на некотором расстоянии z от правого конца балки, изгибающие моменты:

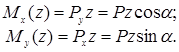
Оба изгибающих момента будут наибольшими в жесткой заделке:

Формула суммарных нормальных напряжений при косом изгибе в произвольном поперечном сечении балки для некоторой точки с координатами x и y:

,

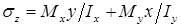где 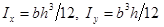– главные моменты инерции; h – высота, а b – ширина поперечного сечения балки. Значения изгибающих моментов и координат исследуемой точки подставляются в формуле нормальных напряжений при косом изгибе по абсолютному значению, а знак каждого из слагаемых определяется по физическому смыслу.

Наибольшие нормальные напряжения при косом изгибе возникнут в поперечном сечении, расположенном в жесткой заделке, в наиболее удаленных от соответствующих нейтральных осей точках 1 и 2:

.

В точке 1 напряжения будут растягивающими: ,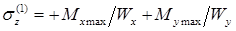

а в точке 2 – точно такими же по величине, но сжимающими: .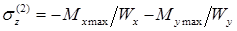

В формулах максимальных нормальных напряжений при косом изгибе 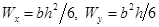– осевые моменты сопротивления балки относительно главных центральных осей инерции.