Переменные во времени напряжения

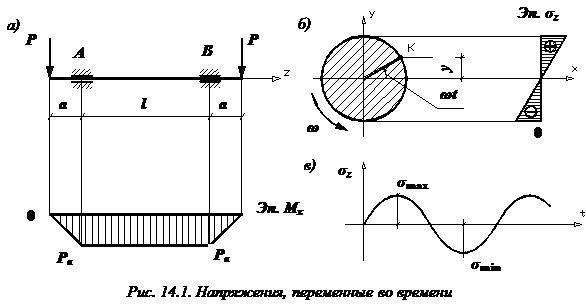
Переменные во времени напряжения рассмотрим на примере оси вагона круглого поперечного сечения диаметром d, нагруженную силами P и вращающуюся с постоянной угловой скоростью 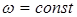(рис. 14.1, а). Подшипники, на которые опирается вал, будем рассматривать как шарнирные опоры.

На участке AB между опорами вал испытывает чистый изгиб (эпюра изгибающих моментов 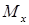построена на сжатых волокнах).

Проследим за изменением нормального напряжения в точке К, расположенной вблизи контура поперечного сечения (рис. 14.1, б). Формула напряжений в произвольной точке поперечного сечения: .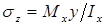

При повороте вала расстояние (y) от точки К до нейтральной оси x будет изменяться от 0 до 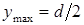. Расстояние точки К до нейтральной оси в некоторый момент времени t может быть определено по формуле:

.

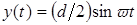Тогда переменные во времени напряжения изменяются по закону:

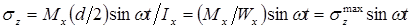
Переменное напряжение в точке К изменяется по синусоидальному закону (рис. 14.1, в). За один полный оборот оси она попадает из зоны растяжения в зону сжатия (или наоборот).

Представим, что к оси вагона помимо сил P (рис. 14.1, а), вызывающих ее изгиб, приложены растягивающие силы 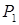. Переменное во времени напряжение в точке К будет равно алгебраической сумме напряжений растяжения и изгиба: .

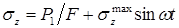График изменения переменных во времени напряжений в рассматриваемой точке K будет представлять собой синусоиду, но смещенную вверх относительно оси t на величину 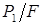.