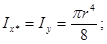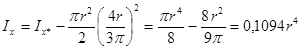Решение задач по сопромату. Геометрические характеристики фигур

Геометрические характеристики фигур / Геометрические характеристики простых фигур: прямоугольника, квадрата, треугольника, круга, полукруга

Результат расчетов зависит не только от площади сечения, поэтому при решении задач по сопромату не обойтись без определения геометрических характеристик фигур: статических, осевых, полярного и центробежного моментов инерции. Обязательно необходимо уметь определять положение центра тяжести сечения (от положения центра тяжести зависят перечисленные геометрические характеристики). К дополнению к геометрическим характеристикам простых фигур: прямоугольника, квадрата, равнобедренного и прямоугольного треугольников, круга, полукруга. Указаны центр тяжести и положение главных центральных осей, и определены относительно них геометрические характеристики при условии, что материал балки однородный.

Геометрические характеристики прямоугольника и квадрата

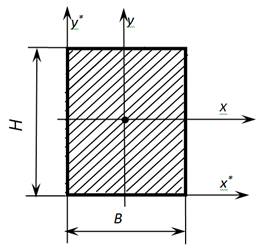
Осевые моменты инерции прямоугольника (квадрата)

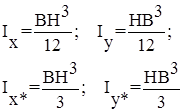
Геометрические характеристики прямоугольного треугольника

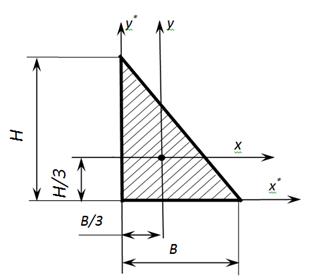
Осевые моменты инерции прямоугольного треугольника

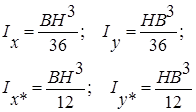
Геометрические характеристики равнобедренного треугольника

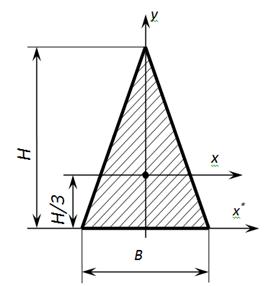
Осевые моменты инерции равнобедренного треугольника

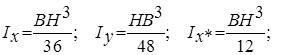
Геометрические характеристики круга

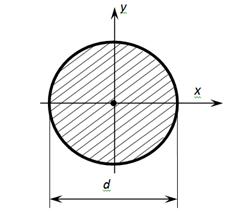
Осевые моменты инерции круга

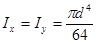
Геометрические характеристики полукруга

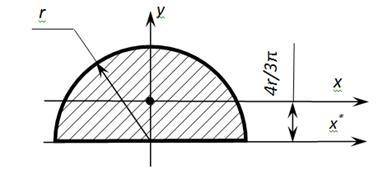
Осевые моменты инерции полукруга