Формула Журавского

Формула Журавского позволяет определить касательные напряжения при изгибе, возникающие в точках поперечного сечении балки, находящиеся на расстоянии от нейтральной оси x.

Вывод формулы Журавского

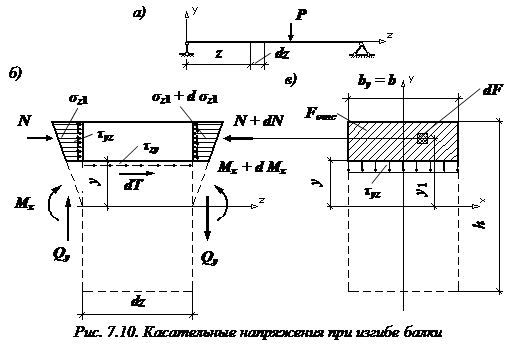
Вырежем из балки прямоугольного поперечного сечения (рис. 7.10, а) элемент длиной 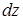и дополнительным продольным сечением рассечем на две части (рис. 7.10, б).

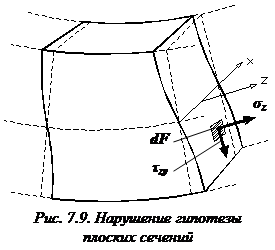
Рассмотрим равновесие верхней части: из-за отличия изгибающих моментов возникают разные сжимающие напряжения. Чтобы эта часть балки находилась в равновесии (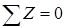) в ее продольном сечении должна возникнуть касательная сила 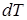. Уравнение равновесия части балки:

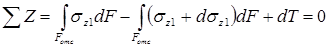
Отсюда

,

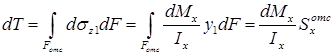где интегрирование ведется только по отсеченной части площади поперечного сечения балки 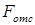(на рис. 7.10, в заштрихована), 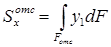– статический момент инерции отсеченной (заштрихованной) части площади поперечного сечения относительно нейтральной оси x.

Предположим: касательные напряжения (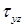), возникающие в продольном сечении балки, равномерно распределены по ее ширине (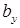) в месте сечения:

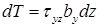
Получим выражение для касательных напряжений:

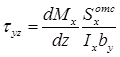
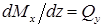, а 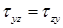, тогда формула касательных напряжений (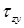), возникающих в точках поперечного сечения балки, находящихся на расстоянии y от нейтральной оси x:

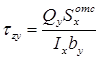- формула Журавского

Формула Журавского получена в 1855 г. Д.И. Журавским, поэтому носит его имя.