Эйлерова нагрузка, формула Эйлера
Л. Эйлер получил формулу для определения теоретической нагрузки (Эйлерова нагрузка), при которой происходит потеря устойчивости стержня. Формула Эйлера: 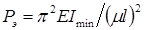 , где Е – модуль Юнга;
, где Е – модуль Юнга; 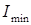 – минимальный главный центральный момент инерции поперечного сечения стержня (очевидно, что при потере устойчивости изгиб стержня произойдет в плоскости наименьшей изгибной жесткости);
– минимальный главный центральный момент инерции поперечного сечения стержня (очевидно, что при потере устойчивости изгиб стержня произойдет в плоскости наименьшей изгибной жесткости); 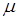 – коэффициент приведения длины, зависящий от формы потери устойчивости; l – длина стержня. Произведение
– коэффициент приведения длины, зависящий от формы потери устойчивости; l – длина стержня. Произведение 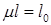 - приведенная длина стержня.
- приведенная длина стержня.
Формула Эйлера для шарнирно-опертого стержня, сжатого по концам
Для шарнирно опертого стержня, сжатого по концам, формула Эйлера для определения критической нагрузки: 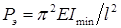 (коэффициент приведения длины
(коэффициент приведения длины 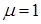 ).
).
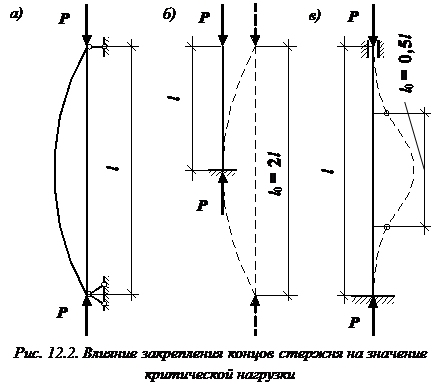
Основной случай потери устойчивости – случай, когда при закреплении концов стержня и приложении нагрузки форма потери устойчивости представляет собой одну полуволну синусоиды (рис. 12.2, а).
Некоторые другие способы закрепления концов стержня (нагрузка по-прежнему приложена по торцам) легко могут быть приведены к основному случаю потери устойчивости путем сопоставления формы изогнутой оси с формой потери устойчивости шарнирно опертого стержня.
Формула Эйлера для стержня с защемленным и свободным концами
При потере устойчивости стержень с жестко защемленным одним и свободным другим концом изогнется, как показано на (рис. 12.2, б). Форма потери устойчивости этого стержня представляет собой четверть синусоиды. Приведенная длина равна 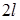 (полуволна синусоиды имеет длину
(полуволна синусоиды имеет длину 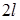 ), а эйлерова сила в четыре раза меньше, чем для основного случая. Формула Эйлера для стержня с защемленным и свободным концами:
), а эйлерова сила в четыре раза меньше, чем для основного случая. Формула Эйлера для стержня с защемленным и свободным концами: 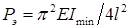 .
.
Формула Эйлера для стержня с защемленными концами
Для стержня, оба конца которого жестко защемлены, форма потери устойчивости такова, что одна полуволна синусоиды занимает половину длины стержня (рис. 12.2, в). Поэтому приведенная длина стержня равна 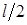 (
(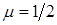 ), а формула эйлеровой нагрузки
), а формула эйлеровой нагрузки 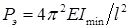 .
.
Критической (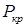 ) принято называть истинную, а эйлеровой (
) принято называть истинную, а эйлеровой (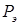 ) – теоретическую нагрузку, при которой происходит потеря устойчивости стержня.
) – теоретическую нагрузку, при которой происходит потеря устойчивости стержня.
Формула Эйлера получена из предположения, что в момент потери устойчивости напряжения сжатия в стержне не превышают предела пропорциональности 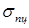 :
: 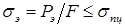 . Модуль Юнга (Е) в формуле Эйлера
. Модуль Юнга (Е) в формуле Эйлера 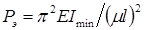 свидетельствует о том, что вплоть до момента потери устойчивости выполнялся закон Гука. Если потеря устойчивости происходит при напряжении меньшем, чем
свидетельствует о том, что вплоть до момента потери устойчивости выполнялся закон Гука. Если потеря устойчивости происходит при напряжении меньшем, чем 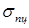 , то
, то 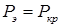 .
.
Для стержней, теряющих устойчивость при напряжении, превышающем предел пропорциональности (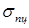 ), использование формулы Эйлера принципиально неправильно и крайне опасно, поскольку критическая нагрузка (истинная нагрузка, при которой происходит потеря устойчивости) меньше эйлеровой нагрузки:
), использование формулы Эйлера принципиально неправильно и крайне опасно, поскольку критическая нагрузка (истинная нагрузка, при которой происходит потеря устойчивости) меньше эйлеровой нагрузки: 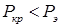 .
.
Пределы применимости формулы Эйлера
Пределы применимости формулы Эйлера можно установить, предварительно введя понятие гибкости стержня. Определим эйлеровы напряжения, исходя из формулы Эйлера: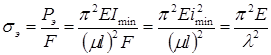 .
.
Здесь 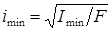 – минимальный радиус инерции;
– минимальный радиус инерции; 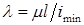 –гибкость сжатого стержня:
–гибкость сжатого стержня: 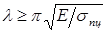 . Величину в правой части неравенства обозначим
. Величину в правой части неравенства обозначим 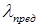 и назовем предельной гибкостью. Тогда
и назовем предельной гибкостью. Тогда 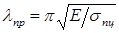 . В отличие от гибкости стержня, предельная гибкость зависит только от физико-механических свойств материала и не зависит от размеров. Предельная гибкость – постоянная для данного материала величина. Например, для стали Ст. 3
. В отличие от гибкости стержня, предельная гибкость зависит только от физико-механических свойств материала и не зависит от размеров. Предельная гибкость – постоянная для данного материала величина. Например, для стали Ст. 3 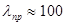 .
.
Используя понятие предельной гибкости, пределы применимости формулы Эйлера можно представить в виде: 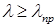 .
.
Формула Эйлера дает истинное значение нагрузки, при которой происходит потеря устойчивости стержня в случае, когда гибкость рассчитываемого стержня больше или равна предельной гибкости для материала, из которого он изготовлен.