Решение типовых задач по сопромату.
Пример решения задачи на расчет статически неопределимых систем при растяжении и сжатии
Расчет статически неопределимых систем при растяжении и сжатии – условие задачи
Для статически неопределимой системы, изображенной на рис. 3.4, а (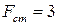 см2;
см2; 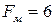 см2;
см2; 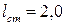 м;
м; 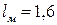 м;
м; 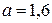 м;
м; 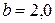 м,
м, 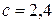 м), требуется определить усилия и напряжения в стальном (
м), требуется определить усилия и напряжения в стальном (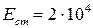 кН/см2;
кН/см2; 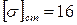 кН/см2) и в медном (
кН/см2) и в медном (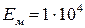 кН/см2;
кН/см2; 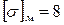 кН/см2) стержнях, выразив их через силу P, а также найти допускаемую нагрузку
кН/см2) стержнях, выразив их через силу P, а также найти допускаемую нагрузку 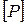 .
.
Расчет статически неопределимых систем при растяжении и сжатии – расчетная схема
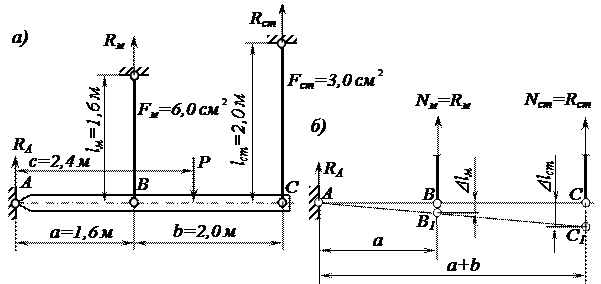 рис. 3.4
рис. 3.4
Расчет статически неопределимых систем при растяжении и сжатии – решение задачи
Находим усилия и напряжения, возникающие в стержнях
Рассечем стержни и изобразим систему в деформированном состоянии (рис. 3.4, б). Под действием силы P абсолютно жесткий на изгиб брус повернется на некоторый малый угол, оставаясь прямолинейным. Поскольку угол поворота абсолютно жесткого на изгиб бруса мал, можно предположить, что его точки В и С будут перемещаться не по дуге окружности, а по вертикали вниз. Деформированное положение системы показано на рис. 3.4, б наклонной прямой линией АС1. Очевидно, что оба стержня, поддерживающие брус, растянутся. Поэтому внутренние усилия 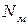 и
и 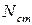 , возникающие в поперечных сечениях этих стержней, направим от сечения. Удлинение медного стержня
, возникающие в поперечных сечениях этих стержней, направим от сечения. Удлинение медного стержня 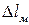 равно отрезку
равно отрезку 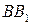 , а стального
, а стального 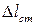 – отрезку
– отрезку 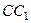 .
.
Для плоской системы параллельных сил мы имеем два независимых уравнения статики. Неизвестных же у нас три: 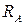 ,
, 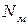 и
и 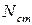 . Следовательно, заданная система является один раз статически неопределимой.
. Следовательно, заданная система является один раз статически неопределимой.
Чтобы исключить из дальнейшего рассмотрения реакцию 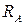 , возникающую в шарнире A, составим следующее уравнение равновесия:
, возникающую в шарнире A, составим следующее уравнение равновесия:
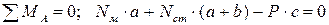 . (3.1)
. (3.1)
В него входят две неизвестные 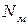 и
и 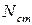 , поэтому для их определения (то есть для раскрытия статической неопределимости) нам необходимо составить еще одно, дополнительное, уравнение.
, поэтому для их определения (то есть для раскрытия статической неопределимости) нам необходимо составить еще одно, дополнительное, уравнение.
Очевидно, что удлинения стержней 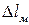 и
и 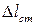 связаны между собой. Из подобия треугольников ABB1 и AСС1 следует, что
связаны между собой. Из подобия треугольников ABB1 и AСС1 следует, что
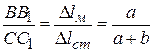 .
.
Или, учитывая закон Гука,
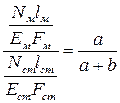 . (3.2)
. (3.2)
Полученное нами дополнительное уравнение (3.2), связывающее деформации стержней, называется уравнением совместности деформаций.
Подставив в (3.1) и (3.2) исходные данные задачи и выполнив несложные преобразования, получим следующую систему уравнений относительно неизвестных внутренних усилий 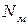 и
и 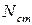 :
:
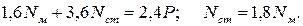
Отсюда находим, что усилия в стержнях равны:
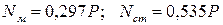 .
.
Тогда напряжения
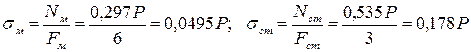 .
.
Определяем допускаемую нагрузку 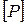
Из условия прочности медного стержня
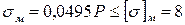 кН/см2
кН/см2
находим, что
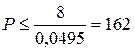 кН.
кН.
Из условия прочности стального стержня
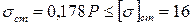 кН/см2
кН/см2
следует, что
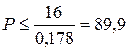 кН.
кН.
Принимая меньшее из найденных выше двух значений, находим, что допускаемая нагрузка для заданной системы равна 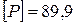 кН.
кН.
Расчет статически неопределимых систем при растяжении и сжатии – задача для самостоятельного решения
Расчет статически неопределимых систем - условие задачи для самостоятельного решения
Горизонтальный абсолютно жесткий на изгиб брус, нагруженный силой P, опирается на шарнирно неподвижную опору и поддерживается двумя упругими стержнями, прикрепленными к нему и к основаниям с помощью шарниров. Один из упругих стержней стальной (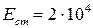 кН/см2;
кН/см2; 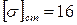 кН/см2), а другой медный (
кН/см2), а другой медный (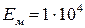 кН/см2;
кН/см2; 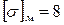 кН/см2) (рис. 3.3). Требуется определить усилия и напряжения, возникающие в стержнях, выразив их через силу P , а также найти допускаемую нагрузку
кН/см2) (рис. 3.3). Требуется определить усилия и напряжения, возникающие в стержнях, выразив их через силу P , а также найти допускаемую нагрузку 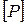 .
.
Расчет статически неопределимых систем при растяжении и сжатии – расчетные схемы к задаче для самостоятельного решения

Расчет статически неопределимых систем при растяжении и сжатии – исходные данные для самостоятельного решения
| Номер схемы | Fст, см2 | Fм, см2 | lст, м | lм, м | a, м | b, м | c, м |
| 1 | 1,0 | 2,0 | 1,0 | 1,0 | 1,0 | 1,0 | 0,5 |
| 2 | 1,0 | 2,0 | 1,0 | 0,8 | 1,0 | 0,8 | 0,6 |
| 3 | 2,0 | 4,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,2 |
| 4 | 3,0 | 5,0 | 1,6 | 1,4 | 1,6 | 1,4 | 1,0 |
| 5 | 4,0 | 6,0 | 1,8 | 1,4 | 1,8 | 1,4 | 1,0 |
| 6 | 2,0 | 4,0 | 1,2 | 1,2 | 1,2 | 1,2 | 0,6 |
| 1 | 2,0 | 3,0 | 1,2 | 1,0 | 1,2 | 1,0 | 0,8 |
| 2 | 3,0 | 4,0 | 1,0 | 1,0 | 1,0 | 1,0 | 1,4 |
| 3 | 4,0 | 5,0 | 1,8 | 1,6 | 1,8 | 1,6 | 1,2 |
| 4 | 5,0 | 6,0 | 2,0 | 1,6 | 2,0 | 1,6 | 1,2 |
| 5 | 3,0 | 4,0 | 1,4 | 1,4 | 1,4 | 1,4 | 0,7 |
| 6 | 3,0 | 5,0 | 1,4 | 1,0 | 1,4 | 1,0 | 0,8 |
| 1 | 4,0 | 5,0 | 1,2 | 1,2 | 1,2 | 1,2 | 1,6 |
| 2 | 5,0 | 7,0 | 2,0 | 1,8 | 2,0 | 1,8 | 1,4 |