Закон Гука формула. Модуль Юнга
Для большинства конструкционных материалов между напряжением (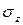 ) и продольной деформацией (
) и продольной деформацией (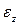 ) до определенного предела нагружения существует линейная зависимость
) до определенного предела нагружения существует линейная зависимость
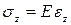
Закон Гука: Напряжение пропорционально деформации.
Впервые Закон Гука был опубликован в виде анаграммы английским ученым Робертом Гуком (1635 – 1703 гг.). При правильной расстановке букв анаграмма читается: «Каково удлинение, такова и сила».
К такому же заключению в 1680 г., независимо от Гука, пришел французский ученый Эдмон Мариотт.
Коэффициент пропорциональности (E) в формуле закона Гука 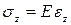 называется модуль продольной упругости или модуль Юнга – по имени английского ученого Томаса Юнга. Значение модуля Юнга для данного материала устанавливается опытным путем. В справочниках обычно приводятся среднее значение модуля Юнга.
называется модуль продольной упругости или модуль Юнга – по имени английского ученого Томаса Юнга. Значение модуля Юнга для данного материала устанавливается опытным путем. В справочниках обычно приводятся среднее значение модуля Юнга.
Необходимо отметить, что некоторые материалы не подчиняются закону Гука, например, кожа, ткани. Такие материалы, как, например, чугун, только с некоторым приближением можно считать подчиняющимся закону Гука. Но даже и те материалы, которые подчиняются закону Гука, перестают ему следовать при достижении деформации определенного значения.
Из закона Гука видно: чем больше модуль Юнга, тем меньше (при том же значении напряжения) деформация материала. Следовательно, модуль продольной упругости характеризует жесткость материала при растяжении (сжатии). Из формулы закона Юнга видно, что модуль Юнга измеряется в тех же единицах, что и нормальное напряжение (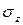 ).
).
Так, например, для всех марок сталей 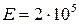 МПа.
МПа.