Коэффициент Пуассона. Связь продольной и поперечной деформации

Пусть в результате деформации первоначальная длина стержня l станет равной. l1. Изменение длины

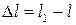
называется абсолютным удлинением стержня.

Отношение абсолютного удлинения стержня к его первоначальной длине называется относительным удлинением (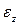 – эпсилон) или продольной деформацией. Продольная деформация – это безразмерная величина. Формула безразмерной деформации:

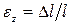
При растяжении продольная деформация считается положительной, а при сжатии – отрицательной.

Поперечные размеры стержня в результате деформирования также изменяются, при этом при растяжении они уменьшаются, а при сжатии – увеличиваются. Если материал является изотропным, то его поперечные деформации равны между собой:

.

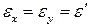Опытным путем установлено, что при растяжении (сжатии) в пределах упругих деформаций отношение поперечной деформации к продольной является постоянной для данного материала величиной. Модуль отношения поперечной деформации к продольной, называемый коэффициентом Пуассона или коэффициентом поперечной деформации, вычисляется по формуле:

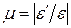
Для различных материалов коэффициент Пуассона изменяется в пределах 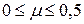. Например, для пробки 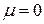, для каучука 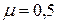, для стали 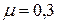, для золота .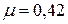