Метод сечений. Силовые факторы в методе сечений
Метод сечений позволяет определить внутренние силы, которые возникают в стержне, находящемся в равновесии под действием внешней нагрузки.
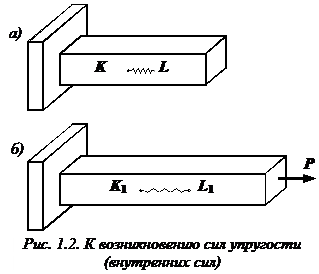
Рассмотрим идеально упругий призматический стержень прямоугольного поперечного сечения (рис. 1.2, а).
Выделим внутри стержня какие-либо две частицы K и L, расположенные на бесконечно малом расстоянии друг от друга. Для большей наглядности предположим, что между этими частицами имеется некоторая пружинка, удерживающая их на определенном расстоянии друг от друга. Пусть натяжение пружинки равно нулю.
 Приложим теперь к стержню растягивающую силу
Приложим теперь к стержню растягивающую силу 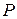 (рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение
(рис. 1.2, б). Пусть в результате деформации стержня, частица K перейдет в положение 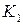 , а частица L – в положение
, а частица L – в положение 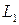 . Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений.
. Соединяющая эти частицы пружинка при этом растянется. После снятия внешней нагрузки частицы вернутся в первоначальное положение K и L благодаря усилию, которое возникло в пружинке. Сила, которая возникла между частицами (в пружинке) в результате деформации идеально упругого стержня, называются силой упругости или внутренней силой. Она может быть найдена методом сечений.
Этапы метода сечений
Метод сечений состоит из четырех последовательных этапов: разрезать, отбросить, заменить, уравновесить.
Разрежем стержень, находящийся в равновесии под действием некоторой системы сил 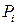 (рис. 1.3, а) на две части плоскостью, перпендикулярной к его оси z.
(рис. 1.3, а) на две части плоскостью, перпендикулярной к его оси z.
Отбросим одну из частей стержня и рассмотрим оставленную часть.
Поскольку мы как бы разрезали бесчисленное множество пружинок, соединявших бесконечно близкие частицы тела, разделенного теперь на две части, в каждой точке поперечного сечения стержня необходимо приложить силы упругости, которые при деформации тела возникли между этими частицами. Иными словами, заменим действие отброшенной части внутренними силами (рис. 1.3, б).
Внутренние силы в методе сечений
Полученную бесконечную систему сил по правилам теоретической механики можно привести к центру тяжести поперечного сечения. В результате получим главный вектор R и главный момент M (рис. 1.3, в).Разложим главный вектор и главный момент на составляющие по осям x, y (главные центральные оси) и z.
Получим 6 внутренних силовых факторов, возникающих в поперечном сечении стержня при его деформировании: три силы 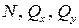 (рис. 1.3, г) и три момента
(рис. 1.3, г) и три момента 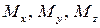 (рис. 1.3, д).
(рис. 1.3, д).
Сила N - продольная сила
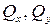 – поперечные силамы,
– поперечные силамы,
момент относительно оси z (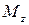 ) – крутящий момент
) – крутящий момент
моменты относительно осей x, y (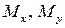 ) – изгибающие моменты.
) – изгибающие моменты.
Запишем для оставленной части тела уравнения равновесия (уравновесим):
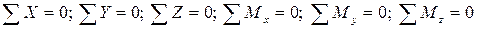 .
.
Из уравнений определяются внутренние усилия, возникающие в рассматриваемом поперечном сечении стержня.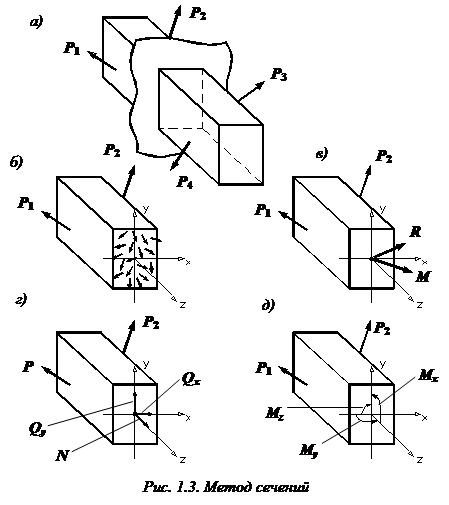
Вычисление продольной и поперечных сил, крутящего и изгибающих моментов
продольная сила N равна сумме проекций всех сил (активных и реактивных), действующих на любую из частей рассеченного стержня, на ось z;
поперечные силы 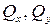 равны сумме проекций всех сил, действующих на любую из частей стержня, на оси x и y, соответственно;
равны сумме проекций всех сил, действующих на любую из частей стержня, на оси x и y, соответственно;
крутящий момент 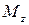 равен сумме моментов всех сил, действующих на любую из частей стержня, относительно продольной оси z;
равен сумме моментов всех сил, действующих на любую из частей стержня, относительно продольной оси z;
изгибающие моменты 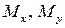 равны сумме моментов всех сил, действующих на любую из частей стержня, относительно осей x и y, соответственно.
равны сумме моментов всех сил, действующих на любую из частей стержня, относительно осей x и y, соответственно.