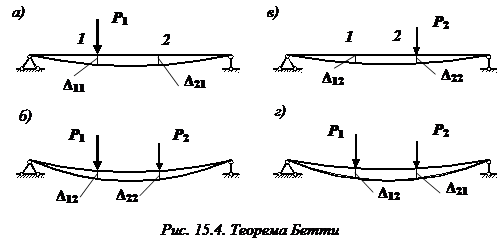
Теорема о взаимности работ (теорема Бетти)

Формулировка теоремы о взаимности работ (теоремы Бетти), доказанная в 1872 г Э. Бетти: возможная работа сил первого состояния на соответствующих перемещениях, вызванных силами второго состояния, равна возможной работе сил второго состояния на соответствующих перемещениях, вызванных силами первого состояния.

Доказательство теоремы о взаимности работ

Наметим на балке две точки 1 и 2 (рис. 15.4, а).

Приложим статически в точке 1 силу 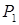. Она вызовет в этой точке прогиб 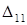, а в точке 2 – .

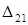Для обозначения перемещений мы используем два индекса. Первый индекс означает место перемещения, а второй – причину, вызывающую это перемещение. То есть, почти как на конверте письма, где мы указываем: куда и от кого.

Так, например, 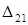означает прогиб балки в точке 2 от нагрузки .

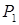После того, как закончен рост силы 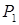. приложим в точке 2 к деформированному состоянию балки статическую силу 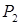(15.4, б). Балка получит дополнительные прогибы: 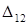в точке 1 и 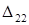в точке 2.

Составим выражение для работы, которую совершают эти силы на соответствующих им перемещениях: .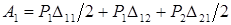

Здесь первое и третье слагаемые представляют собой упругие работы сил 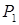и 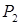. Согласно теореме Клапейрона, они имеют коэффициент 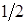. У второго слагаемого этого коэффициента нет, поскольку сила 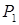своего значения не изменяет и совершает возможную работу на перемещении 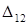, вызванном другой силой .

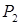Изменим теперь порядок нагружения балки. Сначала прикладываем к балке силу 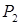, а затем 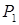(рис. 15.4, в, г).

Тогда работа .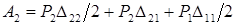

Очевидно, что 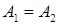. Из этого равенства следует теорема Бетти: .

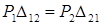Заметим, что теорема Бетти о взаимности работ справедлива как для случая внешних, так и для случая внутренних сил.