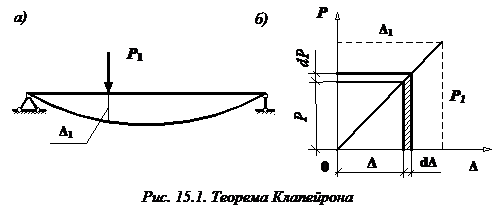
Теорема Клапейрона
Формулировка теоремы Клапейрона: упругая работа внешней силы при статическом приложении равна половине произведения ее окончательного значения на соответствующее этой силе перемещение.
Теорема Клапейрона впервые была сформулирована французским ученым Клапейроном в 1852 г.
|
|
Доказательство теоремы Клапейрона
Определим работу, которую совершает сила 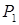 , действующая, например, на балку, изображенную на рис. 15.1, а.
, действующая, например, на балку, изображенную на рис. 15.1, а.
Будем считать, что нагрузка прикладывается к балке статически, то есть она медленно возрастает от нуля до заданной величины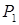 .
.
Пусть в некоторый момент сила, достигшая значения 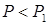 , вызвала в месте своего приложения прогиб балки, равный
, вызвала в месте своего приложения прогиб балки, равный 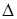 .
.
Увеличим это значение силы на бесконечно малую величину 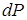 . Такое изменение нагрузки приведет к дополнительному прогибу
. Такое изменение нагрузки приведет к дополнительному прогибу 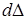 . Очевидно, что элементарная дополнительная работа будет равна:
. Очевидно, что элементарная дополнительная работа будет равна: 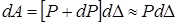 .
.
Полная работа, совершенная внешней силой, определяется по формуле: 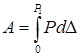 .Для линейно деформируемой системы (график зависимости между прогибом
.Для линейно деформируемой системы (график зависимости между прогибом 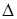 и силой P для такой системы показан на рис. 15.1, б) прогиб балки пропорционален внешней нагрузке, то есть
и силой P для такой системы показан на рис. 15.1, б) прогиб балки пропорционален внешней нагрузке, то есть 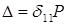 ,
,
где 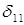 – коэффициент пропорциональности или перемещение от силы, равной единице
– коэффициент пропорциональности или перемещение от силы, равной единице 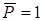 . Коэффициент
. Коэффициент 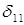 часто называют и податливостью системы.
часто называют и податливостью системы.
Дифференцируя уравнение 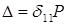 , найдем:
, найдем: 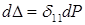 .
.
Подставляя формулу 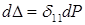 в формулу
в формулу 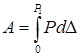 и учитывая уравнение
и учитывая уравнение 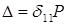 , получим:
, получим: 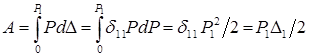 ,что и требовалось доказать. Полученное выражение соответствует теореме Клапейрона.
,что и требовалось доказать. Полученное выражение соответствует теореме Клапейрона.